Class 12 Physics Electric Charges and Fields - Forces between Multiple Charges

Forces Between Multiple Charges – Principle of Superposition

Principle of superposition

Force on any charge due to a number of other charges is the vector sum of all the forces on that charge due to the other charges, taken one at a time. The individual forces are unaffected due to the presence of other charges.

Explanation

Note: Here we are using bold letters to represent vectors.

Consider a system of three charges q₁, q₂, and q₃ with position vectors r₁, r₂, and r₃ respectively as shown in Fig. 1. The forces on q₁ due to q₂ and q₃ are given by F₁₂ and F₁₃ respectively. The resultant force F₁ on q₁ is the vector sum of F₁₂ and F₁₃. The vector sum can be obtained by parallelogram law of vector addition.

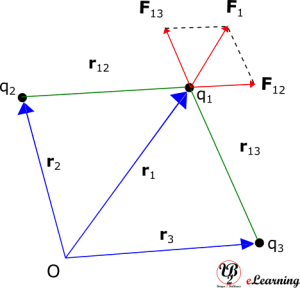
Forces between multiple charges. Principle of Superposition — Fig. 1

By Coulomb’s law of electrostatic force, force on q₁ due to q₂in free space or vacuum is given by

$\mathbf{F}_{12}=\frac{1}{4\pi\varepsilon_0}\frac{q_1q_2}{r_{12}^2}\ {\hat{\mathbf{r}}}_{12}$

Similarly, the force on q₁ due to q₃, is given by

$\mathbf{F}_{13}=\frac{1}{4\pi\varepsilon_0}\frac{q_1q_3}{r_{13}^2}\ {\hat{\mathbf{r}}}_{13}$

The resultant force F₁ on q₁ due to q₂ and q₃ is the vector sum of these two forces. It is given by

$\mathbf{F}_\mathbf{1}=\mathbf{F}_{12}+\mathbf{F}_{13}=\frac{1}{4\pi\varepsilon_0}\frac{q_1q_2}{r_{12}^2}\ {\hat{\mathbf{r}}}_{12}+\ \frac{1}{4\pi\varepsilon_0}\frac{q_1q_3}{r_{13}^2}\ {\hat{\mathbf{r}}}_{13}$

Like that if there are n charges and the force on charge q₁ due to all other charges is given by

$\mathbf{F}_\mathbf{1}=\mathbf{F}_{\mathbf{12}}+\mathbf{F}_{\mathbf{13}}+\ldots+\mathbf{F}_{\mathbf{1n}}=\frac{1}{4\pi\varepsilon_0}\frac{q_1q_2}{r_{12}^2}\ {\hat{\mathbf{r}}}_{\mathbf{12}}+\frac{1}{4\pi\varepsilon_0}\frac{q_1q_3}{r_{13}^2}\ {\hat{\mathbf{r}}}_{\mathbf{13}}+\ldots+\frac{1}{4\pi\varepsilon_0}\frac{q_1q_n}{r_{1n}^2}\ {\hat{\mathbf{r}}}_{\mathbf{1n}}=\frac{1}{4\pi\varepsilon_0}q_1\sum_{i=2}^{n}\frac{q_i}{r_{1i}^2}{\hat{\mathbf{r}}}_{\mathbf{1i}}$

Numerical

Q. Calculate force on any charge q, if three equal and similar charge +q is placed at the edges of an equilateral triangle.

Solution:

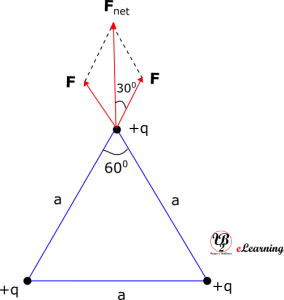
Force between multiple charges. Principle of superposition — Fig. 2

Force on one charge due to other two charges are given by Coulomb’s law of electrostatic force. Since charges are same which is q, and distance between them are also same as they are placed at the sides of equilateral triangle. So, forces are same in magnitude and is given by,

$F=k\frac{q^2}{a^2}$

Direction of forces are as shown in Fig. 2.

The resultant force is the vector sum of these two forces, the magnitude of the net force is given by the equation,

$F_{net}=\sqrt{F^2+F^2+2FF\ Cos\ 60}=\sqrt{2F^2+2F^2\times\frac{1}{2}}=\sqrt3\ F$

We also know, if the vectors with equal magnitude makes an angle $\theta$ with each other, then the resultant vector will bisect the angle between them. That is the resultant vector makes an angle $\theta/2$ from both vectors.