Class 12 Physics Electric Charges and Fields – Coulomb’s Law

---

---

Forces between Two Point Charges – Coulomb’s Law, Coulomb’s Law in Vector Form

[Watch Video to Understand in Detail and in Malayalam Language]

Coulomb’s Law

Coulomb’s law states that the force between two point charges varied inversely as the square of the distance between the charges and was directly proportional to the product of the magnitude of the two charges and acted along the line joining the two charges.

Thus, if two point charges q₁, q₂ are separated by a distance r in vacuum, the magnitude of the force (F) is

 and 

In free space or vacuum the value of constant k

is called the permittivity of free space. The value of in SI units is

So that Coulomb’s law is written as

The Coulomb’s law and the value of  gives us an idea about SI unit of charge coulomb. Let q₁ = q₂ = 1 C and r = 1 m, then force

That is, 1 C is the charge that when placed at a distance of 1 m from another charge of the same magnitude in vacuum experiences an electric force of repulsion of magnitude 9 X 10⁹ N. 1 C is too big unit to be used. In practice, in electrostatics, one uses smaller units like 1 mC or 1 µC.

---

Coulomb’s law in Vector Notation

Since force is a vector, we have to write Coulomb’s law in the vector notation [Note: here we are using bold letters to represent vectors]. Let the position vectors of charges q₁ and q₂ be r₁ and r₂ respectively. The resultant vector leading from q₁ to q₂ is denoted by

r₂₁ = r₂ – r₁

And the vector leading from q₂ to q₁ is denoted by r₁₂:

r₁₂ = r₁ – r₂ = – r₂₁

The unit vectors along this can be represented as:

Also force on q₁ due to q₂ by F₁₂ and force on q₂ due to q₁ by F₂₁.

Coulomb’s force law between two point charges q₁ and q₂ located at r₁ and r₂ in vacuum or free space is then expressed as

See figure for geometric representation.

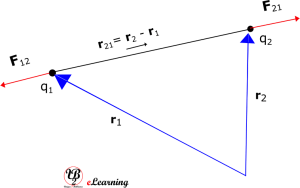
The above diagram is for q₁ x q₂ > 0, the force is repulsive in nature. If q₁ x q₂ < 0, the force is attractive in nature and figure below shows that.

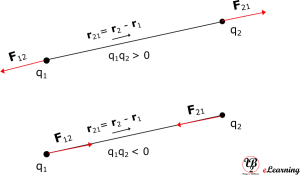
Some points related to Coulomb’s law in vector notation are as follows:

It is valid for any sign of q₁ and q₂ whether positive or negative. If q₁ and q₂ are of the same sign (either both positive or both negative), F₂₁ is along , which denotes repulsion, as it should be for like charges. If q₁ and q₂ are of opposite signs, F₂₁ is along , which denotes attraction, as expected for unlike charges. That is equation is true for both cases correctly.

It also proves that Coulomb’s law agrees with Newton’s third law.

The force F₁₂ on charge q₁ due to charge q₂, is obtained by simply interchanging 1 and 2 in the above equation, i.e.,

---