Class 12 Physics Electric Charges and Fields – Electric Field

Leave a Comment / By /
Subscribe to Us on Youtube

Previous <<< Forces Between Multiple Charges – Principle of Superposition

Topics in Chapter 1 – Electric Charges and Fields

Electric Field

[Watch Video for Detailed Explanation]

Electric Field due to a charge or system of charges is the space around it where any other charges experience an electrostatic force.

Intensity of electric field is the measure of electric field. Intensity of electric field at a point is measured by force being experienced by a charge. Most often we call intensity of electric field as electric field only. It is represented as E.

If we are placing a charge q at a point without disturbing other charges which produce electric field, the force is given by,

F = qE

That is,

E = F/q

That is force per unit charge gives the intensity of electric field.

SI unit of electric field is N/C

The charge which producing the electric field, is called a source charge and the charge which tests the effect of a source charge is called a test charge.

The test charge q must be very small in its magnitude to avoid force on source charge by the test charge and thus change the electric field. That is q tends to zero.

Here we know force is a vector quantity, so electric field is also a vector quantity. And the direction of electric field is same as the direction of force if the test charge is positive and opposite to the force if the test charge is negative.

For a positive charge, the electric field will be directed radially outwards from the charge. And for negative charge, the electric field vector, at each point, points radially inwards.

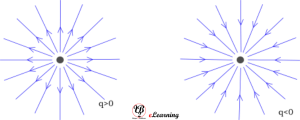
Direction of Electric field due to a positive charge and for a negative charge. Class 12 Physics Chapter 1 - Electric Charges and Fields
Fig. 1

Electric Field due to a point charge

Consider a point charge Qplaced at a point A. The force exerted on another point charge q at a point P, where AP = r, due to the charge Q is given by Coulomb’s law.

\mathbf{F}=k\frac{Qq}{r^2}\ \hat{\mathbf{r}}

The electric field is given by the equation E = F/q

Therefore,

\mathbf{E}=\frac{\mathbf{F}}{q}\ =k\frac{Q}{r^2}\ \hat{\mathbf{r}}

Where, \hat{\mathbf{r}}=\mathbf{r}/r , is a unit vector from point A to the point P. This is the electric field produced by the charge Q at a point P distance r from source charge.

If position vector from origin to source charge is rA and position vector of point P from origin is rP, then vector r = rP – rA. The equation for electric field can be generalized as,

\mathbf{E}=k\frac{Q}{r^2}\hat{\mathbf{r}}\ =k\frac{Q}{r^3}\ {(\mathbf{r}}_{P\ }-\ \mathbf{r}_A)

Note: In this formula substitute q with sign.

If it is in free space k=\frac{1}{4\pi\varepsilon_0}

Thus, the electric field due to a charge Q at a point in space may be defined as the force that a unit positive charge would experience if placed at that point.

The magnitude of the electric field E will depend only on the distance r. Thus at equal distances from the charge Q, the magnitude of its electric field E is same. The magnitude of electric field E due to a point charge is thus same on a sphere with the point charge at its centre; in other words, it has a spherical symmetry.

Electric field due to a system of charges

Electric field at a point in space due to a system of charges is also defined to be the force experienced by a unit test charge placed at that point, without disturbing the original positions of charges.

Remember the test charge must be very small so that it must not disturb the position of charges, and thus electric field.

By using superposition principle, we can write the electric field at a point due to a system of charges is the vector sum of individual electric fields due to the charges at that point. An example of three charges is shown in figure below (Fig. 2).

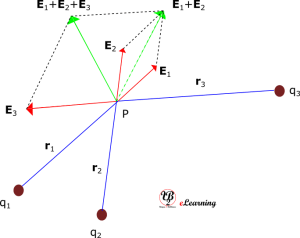
Electric Field Due to a System of Charges. Class 12 Physics Chapter 1 - Electric Charges and Fields
Fig. 2

Consider a system of charges q1, q2, and q3

Electric field E1 at Pdue to q1 is given by

\mathbf{E}_1=k\frac{q_1}{r_1^2}\ {\hat{\mathbf{r}}}_1

where {\hat{\mathbf{r}}}_1 is a unit vector in the direction from q1 to P, and r1 is the distance between q1 and P.

Similarly,

\mathbf{E}_2=k\frac{q_2}{r_2^2}\ {\hat{\mathbf{r}}}_2\ and\ \mathbf{E}_3=k\frac{q_3}{r_3^2}\ {\hat{\mathbf{r}}}_3

By the superposition principle, the electric field E at Pdue to the system of charges is the vector sum of individual electric fields. That is,

\mathbf{E}_1+\mathbf{E}_2+\mathbf{E}_3=k\frac{q_1}{r_1^2}{\hat{\mathbf{r}}}_1+k\frac{q_2}{r_2^2}{\hat{\mathbf{r}}}_2+k\frac{q_3}{r_3^2}{\hat{\mathbf{r}}}_3

Generalizing for n charges

\mathbf{E}=\mathbf{E}_1+\mathbf{E}_2+\ldots+\mathbf{E}_n=k\frac{q_1}{r_1^2}{\hat{\mathbf{r}}}_1+k\frac{q_2}{r_2^2}{\hat{\mathbf{r}}}_\mathbf{2}+\ldots+k\frac{q_n}{r_n^2}{\hat{\mathbf{r}}}_\mathbf{n}=k\sum_{i=1}^{n}\frac{q_i}{r_i^2}{\hat{\mathbf{r}}}_\mathbf{i}

In free Space k=\frac{1}{4\pi\varepsilon_0}

Leave a Comment

Your email address will not be published. Required fields are marked *